Introduction

Many of the ideas now being developed in the framework of Support Vector Machines were first proposed by V. N. Vapnik and A. Ya. Chervonenkis (Institute of Control Sciences of the Russian Academy of Sciences, Moscow, Russia) in the framework of the “Generalised Portrait Method” for computer learning and pattern recognition. The development of these ideas started in 1962 and they were first published in 1964 [1].

Support Vector Machines are supervised learning models with associated learning algorithms that analyse data used for classification and regression analysis.

The support vector (SV) machine implements the following idea: It maps the input vectors x into a high-dimensional feature space Z through some nonlinear mapping, chosen a priori. In this space, an optimal separating hyperplane is constructed.

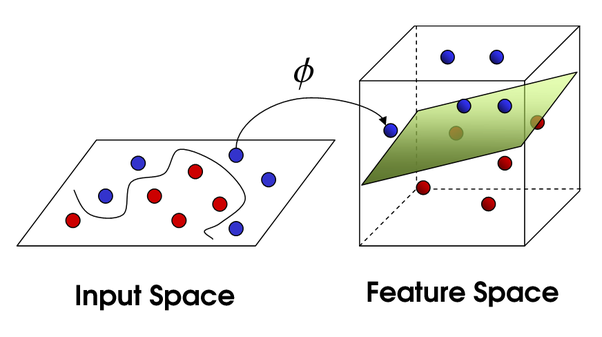
(C. Moreira, "Learning To Rank Academic Experts", Master Thesis, Technical University of Lisbon, 2011.)

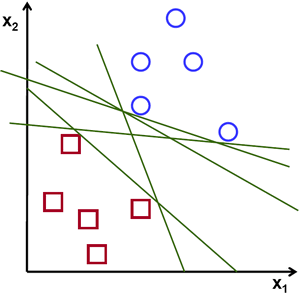
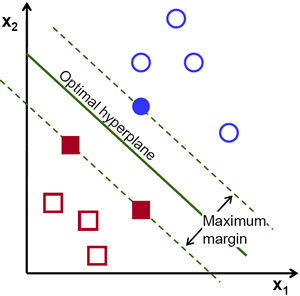
The original maximum-margin hyperplane algorithm proposed by Vapnik in 1963 constructed a linear classifier. In 1992, Boser, Guyon and Vapnik suggested a way to create nonlinear classifiers by applying the kernel trick to maximum-margin hyperplanes. The resulting algorithm is formally similar, except that every dot product is replaced by a nonlinear kernel function. This allows the algorithm to fit the maximum-margin hyperplane in a transformed feature space. The transformation may be nonlinear and the transformed space high dimensional; although the classifier is a hyperplane in the transformed feature space, it may be nonlinear in the original input space [7].